일원분산분석(One-Way ANOVA)

Research Methodologies & Statistics

일원분산분석(One-Way ANOVA)

VTAOE 2022. 4. 13. 05:33

install.packages("ggplot2")
library(ggplot2)

분산분석 I

흔히 One-Way ANOVA를 일원분산분석 또는 일원배치분산분석이라고 한다(이하 일원분산분석). 분산분석은 3개 혹은 그 이상의 집단 간 평균을 비교하는 것으로 독립변수는 집단을 나타내야하고 종속변수는 연속변수이어야 한다. 참고로 일원분산분석은 한개의 독립변수를, 이원분산분석은 두개의 독립변수를 사용하는 것이다.

분산분석을 함에 있어 중요한 세가지의 가정이 있는데 1. 독립성, 2.정규성, 3.등분산성이다.

첫째 독립성은 독립변수에 있는 하위 집단들은 서로 독립적이어야 한다는 것이다. 이 가정은 분석 단계가 아닌 표본을 추출하는 단계에서 충족시켜져야 한다.

두번째는 정규성으로 독립변수에 따른 종속변수는 정규분포를 이뤄야 한다는 가정으로 Q-Q plot, Shapiro-Wilk검정, 혹은 K-S 검정으로 확인할 수 있다.

세번째는 등분산성으로 모든 집단의 분산은 동일하다는 가정으로 Levene test 혹은 Bartlett test로 확인할 수 있고 또 다른 방법은 표준편차 값을 이용해서 확인 할 수 있다. 두번째와 세번째의 경우는 뒤에서 다시 살펴보았다.

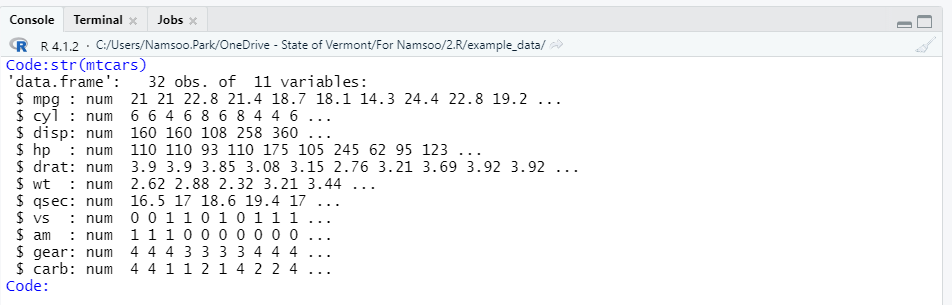
일원분산분석을 살펴보기 위하여 데이터는 mtcars 데이터를 사용하였고 mtcars 데이터의 구조를 살펴보면

str(mtcars)

일원분산분석을 살펴보기 위해 mpg를 종속변수로, 독립변수로 gear를 사용하였다.

[가설-정규성]

먼저 정규성을 검증하기 위하여 shapiro test를 시행하였다. 영가설은 종속변수가 정규분포를 이룬다는 것이고, 연구가설은 정규분포를 이루지 않는다는 것이다. 그러므로 p-value가 .05보다 커야 연구가설을 채택하지 않을 수 있다.

shapiro.test(mtcars$mpg)


	Shapiro-Wilk normality test

data:  mtcars$mpg
W = 0.94756, p-value = 0.1229

p-value가 .05보다 크므로 정규분포를 이룬다고 볼 수 있다.

콜모고르프-스미로노프 검정은 표본수가 많을때 사용하는 것으로 p-value가 .05보다 크면 영가설을 기각할 수 없기 때문에 정규분포를 이룬다고 본다.

ks.test(mtcars$mpg, "pnrom", mean=mean(mtcars$mpg), sd=sd(mtcars$mpg))


	One-sample Kolmogorov-Smirnov test

data:  mtcars$mpg
D = 0.1263, p-value = 0.687
alternative hypothesis: two-sided

역시 p-value가 .05보다 크므로 영가설을 기각할 수 없다. 그러므로 정규분포를 이룬다고 볼 수 있다.

[가설-등분산성]

등분산성을 검정하기 위하여 Levene 테스트를 먼저 시행하였다. Levene 테스트를 하기 위해서는 lawstat 패키지를 설치한 후 로드해야 한다. 아래에서는 Location을 설정하지 않았기 때문에 Brown-Forsythe Levene 테스트 결과가 제시되었고, p-value가 .05보다 크므로 모든 집단의 분산에는 차이가 없다는 영가설을 기각 할 수 없었다. 그러므로 등분산성 가정을 충족한다고 볼 수 있다.

install.packages("lawstat")
library(lawstat)

levene.test(mtcars$mpg, mtcars$gear)


	Modified robust Brown-Forsythe Levene-type test
	based on the absolute deviations from the median

data:  mtcars$mpg
Test Statistic = 1.4886, p-value = 0.2424

만약 location="mean"을 입력해주면 Classical Levene test 결과가 제시된다. 이 역시도 p-value가 .05보다 크므로 영가설을 기각할 수 없고 등분산성을 충족한다고 볼 수 있다. 고

levene.test(mtcars$mpg, mtcars$gear, location="mean")

    Classical Levene's test based on the absolute
	deviations from the mean ( none not applied because
	the location is not set to median )

data:  mtcars$mpg
Test Statistic = 3.1937, p-value = 0.05578

두번째 방법은 Bartlett 테스트를 시행하는 것이다. 이 역시도 p-value가 0.5보다 크므로 등분산성을 만족한다고 볼 수 있다. 참고로 Bartlett 테스트는 정규성을 만족할 때만 사용할 수 있는 것으로 이 점이 Levene 테스트와 다른 점이다.

bartlett.test(mtcars$mpg, mtcars$gear)
## bartlett.test(mpg~gear, mtcars) 

	Bartlett test of homogeneity of variances

data:  mtcars$mpg and mtcars$gear
Bartlett's K-squared = 3.8253, df = 2, p-value =
0.1477

마지막 방법으로 표준편차를 이용하는 방법인데 가장 큰 값과 가장 작은 값의 비율이 2보다 작으면 등분산성을 만족한다고 본다.(ref: Davis, T.M. (2016). The book of R : a first course in programming and statistics.) 비교 결과 1.975로 2보다 작으므로 등분산성을 만족한다고 볼 수 있다.

mpg.sd <- tapply(mtcars$mpg, INDEX=mtcars$gear, FUN=sd)
max(mpg.sd)/min(mpg.sd)

[1] 1.97501

가정에 대한 검증이 끝났으므로 분산분석을 시행하였다. 독립변수는 gear, 종속변수는 mpg이고 데이터는 mtcars이다. 분산분석을 하기에 앞서 사후검정을 위하여 gear변수를 numeric에서 factor변수로 변형해 주었다. 이때 mtcars 데이터를 새로운 데이터 이름(mtcars_new)에 할당한 후 진행하였다.

mtcars_new <- mtcars
mtcars_new$gear <- factor(mtcars_new$gear)

분산분석을 위한 기본 코드는 aov(종속변수~독립변수, data=데이터명)이고 요약된 결과를 보기 위해서는 summary()를 이용하면 된다.

mpg.anova <- aov(mpg~gear, data=mtcars_new)
summary(mpg.anova)


            Df Sum Sq Mean Sq F value Pr(>F)   
gear         1  259.7  259.75   8.995 0.0054 **
Residuals   30  866.3   28.88                  
---
Signif. codes:  
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

F=8.995, p=.0054로 유의수준 .05보다 작으므로 gear에 따라 mpg가 통계적으로 유의미한 차이가 있다고 볼 수 있다. 그러나 우리는 어떤 집단 간에 차이가 있는지 모르기 때문에 사후검정을 해야 한다.

사후검정에는 여러가지가 있는데 가지고 있는 데이터의 특성에 따라 선택해 주면 된다.

먼저 TukeyHSD방법에 대해서 살펴보았다.

TukeyHSD(mpg.anova)

 Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = mpg ~ gear, data = x)

$gear
         diff        lwr       upr     p adj
4-3  8.426667  3.9234704 12.929863 0.0002088
5-3  5.273333 -0.7309284 11.277595 0.0937176
5-4 -3.153333 -9.3423846  3.035718 0.4295874

gear가 4인 집단의 평균 mpg가 gear가 3인 집단의 평균 mpg보다 크고 이 차이는 통계적으로 유의미한 것을 알 수 있다(diff = 8.426, p adj = .0002). gear가 5인 집단의 평균 mpg가 gear가 3인 집단의 평균 mpg보다는 크지만 통계적인 유의미성을 찾을 수 없었고(diff=5.273, p adj = .093), gear가 5인 집단의 평균 mpg가 gear가 4인 집단의 평균 mpg보다 작지만 이 역시도 통계적인 유의미성을 찾을 수 없었다(diff=-3.153, p adj = .4295).

두번째 살펴볼 방법은 scheffe 방법으로 집단간 표본의 수가 차이가 있을때 사용할 수 있는 방법이다.

install.packages("agricolae")
library(agricolae)

scheffe.test(mpg.anova,"gear",console=TRUE)

"agricolae" 패키지를 설치 한 후 scheffe.test(mpg.anova,"gear",console=TRUE)를 실행하여 사후검정을 할 수 있지만, TukeyHSD, Bonferroni, Scheffe, Fisher의 LSD 방법을 모두 할 수 있는 간편한 페키지 "DescTools"가 있다.

install.packages("DescTools")
library(DescTools)

PostHocTest(mpg.anova, method='scheffe')


### result

  Posthoc multiple comparisons of means: Scheffe Test 
    95% family-wise confidence level

$gear
         diff     lwr.ci    upr.ci    pval    
4-3  8.426667  3.7226373 13.130696 0.00033 ***
5-3  5.273333 -0.9987059 11.545373 0.11305    
5-4 -3.153333 -9.6184034  3.311737 0.46265

사후검정을 할 때 method='사후검정명'만 바꿔주면 된다.

PostHocTest(mpg.anova, method='scheffe') ##Scheffe's method
PostHocTest(mpg.anova, method='hsd') ##TukeyHSD
PostHocTest(mpg.anova, method='lsd') ##Fisher's LSD
PostHocTest(mpg.anova, method='bonferroni') ## Bonferroni correction