단일 모집단평균에 대한 가설 검정/일표본 t검정/t-test (2)

carfuel.csv

0.00MB

앞선 단일 모집단평균에 대한 가설 검정/일표본 t검정/t.test (1)에서는 t.test 명령어를 이용하여 분석하는 법을 살펴보았다. 이번 장에서는 각 단계별로 어떻게 계산되어지는지 그 절차를 살펴보고자 한다. 

 

영가설은 ㄱ 자동차의 연비는 리터당 30km이다 이고, 연구가설은 리터당 30km가 되지 않는다였다. 

가설을 검정하기 위하여 80대의 자동차를 무선으로 표집했으므로 n = 80이 된다.

 

표본평균을 구해보면 26.6이다. 첨부된 파일이 데이터프레임의 형태이기 때문에 mean(데이터&변수명)을 입력해줘야 한다.

car.mean <- mean(ex$x)
round(car.mean,1)

[output]
> round(car.mean,1)
[1] 26.6

표본의 표준편차를 구해보면 3.3이다.

car.sd <- sd(ex$x)
round(car.sd, 1)

[output]
> round(car.sd, 1)
[1] 3.3

표본의 평균을 보면 26.6으로 80대 자동차의 평균 연비가 리터당 26.6km라고 볼 수 있는데 과연 이 값이 유의미한 것인지 살펴보고자 하는 것이다.

 

다음으로 계산해야 할 것이 통계치값이다. T값을 구하는 공식은 다음과 같다

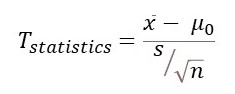
- (표본의 평균 - 모집단의 평균) : 26.6 - 30

- (표본의 표준편차/n의 제곱근) : 3.3/80의 제곱근 즉, 표본의 표준오차이다

 

표준오차는 앞서 구한 표본의 표준편차인 car.sd /sqrt(사례수)로 계산할 수 있다. 그 결과 0.4이다.

car.se <- car.sd/sqrt(80)
round(car.se, 1)

[output]
> car.se <- car.sd/sqrt(80)
> round(car.se, 1)
[1] 0.4

여기까지 구했으면 우리는 검정통계량 T값을 계산할 수 있고 검정통계량 T값은 -9.0583이다.

car.t <- (car.mean-30)/(car.se)
car.t

[output]
> car.t <- (car.mean-30)/(car.se)
> car.t
[1] -9.058313

t값(임계치)은 유의수준이 0.1일 때는 1.66, 0.05일때는 1.98, 0.01일때는 2.63임을 알고 있으면 굳이 t분포표를 보지 않아도 쉽게 연구가설 채택 여부를 알 수 있다.

 

주어진 조건에서 임계치 값을 구할 수 있는데 유의수준은 0.05, 자유도(df) = n-1 = 79이므로 아래의 코드를 실행하면 -1.66임을 알 수 있다. 만약 오른쪽 검정(30km보다 연비가 높다 라고 한다면 qt(1-0.05, df=79)를 입력해야 한다.

qt(0.05,df=79)

[output]
> qt(0.05, df=79)
[1] -1.664371

우리가 구한 t값이 -9.06이고, t임계치가 -1.66이므로 우리가 구한 검정통계량 t값이 -1.66보다 작은 것을 알 수 있다. 이런 경우 우리는 연구가설을 채택할 수 있다. 만약 검정통계량 t값이 임계치 값보다 크면 연구가설을 채택할 수 없다. 

 

이렇게  검정통계량 T값을 이용해서 연구가설 채택 여부를 확인할 수 있고 그 다음으로는 p-value가 유의수준보다 작은지 큰지에 따라 연구가설 채택여부를 확인 할 수 있다. 그러면 p-value를 계산해보는 방법을 살펴보고자 한다. 그 결과 유의수준 0.05보다 훨씬 작은 것을 알수 있다. 그러므로 우리는 영가설을 기각하고 연구가설을 채택할 수 있다. 

pt(car.t, df=79)

[output]
> pt(car.t, df=79)
[1] 3.74229e-14

마지막으로 신뢰수준을 구해보았다. 신뢰수준은 상한값과 하한값이 주어지기 때문에 단측검정이 아닌 양측검정을 기준으로 한다. 그러므로 만약 유의수준이 0.05였다면 하한값 쪽에 0.025, 상한값 쪽에 0.025의 구간이 정해지게 된다. 

confidence Interval에 모집단 평균이 30km가 포함되지 않음을 알 수 있다.  

car.mean+c(-1,1)*qt(0.975, n-1)*car.se

[output]
> car.mean+c(-1,1)*qt(0.975, n-1)*car.se
[1] 25.91235 27.38515

특별히 각 단계의 값을 구하는 것이 아니라면 t.test 명령어를 사용하는 것이 손쉽게 결과를 구할 수 있지만, 어떻게 결과가 도출되는지에 대한 단계를 이해하기 위해 각 단계별로 계산해보았다. 통계를 조금 더 쉽게 공부하고자 하는 분들은 시중에 많은 책들이 나와있지만 특별히 이훈영교수의 통계학 책을 추천드린다. 제가 통계에 대한 지식 없는 가운데에서 통계를 처음 배우고 싶을 때 접했던 책인데 자세하게 설명이 되어 있어서 많은 도움을 받았다.